Team Round #11: 第十六届浙江大学宁波理工学院程序设计大赛重现赛

发表于 更新于 分类于 阅读次数： 评论数：
本文字数： 1.5k 阅读时长 ≈ 5 分钟
本文记录了Daenerys Stormborn of the House Targaryen.的第11场训练

这一场是在2019-12-07 13:00:00 至 2019-12-07 17:00:00打的。

宁波理工的题 个人觉得还是很好的。总能学到一些东西！而不是都是模拟题搞人心态让人自闭。

队伍第一次实施分题目补题，在语雀上进行共同编辑。这样方便大家学习。
事实上，语雀的md用不太习惯，或许是我一直以来用VSC写md的原因，没用typora。。直接搬过来还是有点格式上的问题。不过也由于懒只是稍微fix一下…

• 传送门
• 题解链接

E. 雷顿女士与平衡树

首先题目显然可以将最大值和最小值分为两部分分别计算。
求最大值的方法：从小到大将每个点与相连的点用并查集合并，同时维护每个联通块的size，此时显然可以计算此点作为最大值的路径条数。

• 分成最大值和与最小值和分别进行求解, 然后相减得到答案

求最大值方法

  1. 首先node中储存边的两个点编号x, y, 两点权值的最大值v
  2. 读入所有边, 储存在 maxNode
  3. 按 v 从小到大遍历 maxNode , 保证当前为最大值, 以下为循环中内容:
    a. 分为左右两个连通块, 联通块的size用 并查集 维护
    • 两连通块的size设为 a 和 b
    b. 以当前 node.v 为最大值的所有路径的数量为
    • a b
    c. 最大值的和为
    • (a     b) * v
    d. 合并两个连通块
    e. 不断进行累加即可得到所需要的最大值
  4. 最小值同理
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    #include <bits/stdc++.h>
    using namespace std;
    typedef long long ll;
    const ll nmax = 5e5 + 5;
    const ll mod = 1e9 + 7;
    struct node {
        ll x, y, v;
    }maxNode[nmax], minNode[nmax];
    ll n, e;
    ll a[nmax];
    int fa[nmax];
    int cnt[nmax];
    void init(){
        for(int i = 0; i < n; i++){
            fa[i] = i;
            cnt[i] = 1;
        }
    }
    int find(int x){
        return x == fa[x] ? x : fa[x] = find(fa[x]);
    }
    void uni(int x, int y){
        fa[x] = y;
        cnt[y] += cnt[x];
    }
    int main() {
        std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
        int t;
        cin >> t;
        while(t--){
            cin >> n;
            e = n - 1;
            for(int i = 0; i < n; i++) cin >> a[i];
            int x, y;
            for(int i = 0; i < e; i++){
                cin >> x >> y;
                x--;
                y--;
                maxNode[i] = node{x, y, max(a[x], a[y])};
                minNode[i] = node{x, y, min(a[x], a[y])};
            }
            sort(maxNode, maxNode + e, [](node& a, node& b){
                return a.v < b.v;
            });
            sort(minNode, minNode + e, [](node& a, node& b){
                return a.v > b.v;
            });
            init();
            ll maxsum = 0;
            for(int i = 0; i < e; i++){
                int curx = find(maxNode[i].x);
                int cury = find(maxNode[i].y);
                maxsum = (maxNode[i].v * cnt[curx] % mod * cnt[cury] % mod + maxsum) % mod;
                uni(curx, cury);
            }
            init();
            ll minsum = 0;
            for(int i = 0; i < e; i++){
                int curx = find(minNode[i].x);
                int cury = find(minNode[i].y);
                minsum = (minNode[i].v * cnt[curx] % mod * cnt[cury] % mod + minsum) % mod;
                uni(curx, cury);
            }
            ll ans = (maxsum - minsum + mod) % mod;
            cout << ans << endl;
        }
        return 0;
    }

G. 雷顿女士与多米诺骨牌

题解方法有点迷，分成两个图后上我的想法是两层图后都将所有点都拆开，并且按照题解的意思，对于（i+j)&1的点第一层点后第二层当前点对应的点的入点相连，而同一层，遍历四个方向，若不是则该点出点连接那个点的入点，而对于!((i+j)&1)的点，对于第二层的点按照之前同样的操作与第一层对应的点的入点和自身周围的点相连，随后建立超级源点S和每一个第一层(i+j)&1和第二层!((i+j)&1)的入点相连，并且建立超级汇点T让所有每层没有与超级源点相连的点的出点连接T，对于#的点不建立竖直方向的边，对于的点只建立竖直方向的边，随后费用流，得到的结果应该与题解意思一样是两倍的答案，但。。。spfa给卡死循环了（可能写出了负环。。。），至此不知道哪出问题了。
随后学习全场唯一一个过的代码，首先建图，由于是要跑最大费用流，因此将所有点的权值取反是肯定的，其次对于#的点是必须要覆盖的点，所以可以将它的权值减去inf，他的优先级在跑spfa时是可以体现出来的，是一定可以松弛从S到T路径的（除非这条路不连通），若这条路不连通，或者是由于流量的限制导致无法完全将所有#都覆盖，这时给必过点权值减inf又带来了第二个好处->所跑出的minMaxflowCost的结果加上cnt（必过点个数）inf是大于1000n*m的（一个inf足够大）。

但这远远不能解这个题，因为这个题并不需要跑出maxflow，仅仅需要求得覆盖的最大权重和，因此在题解中给出了建立双层的图，因为通过双层图可以保证一定跑出maxflow（最差所有点连接与自身相对应的点），所以产生了取消费用流流量优先的性质，而这个代码中第二重要的关键部分就是这个dist[t]>=0即返回不可松弛，因为在spfa中判断时是第一满足当前边不满流，第二满足路径可以松弛，可以设想一种情况就是流是没有满，但是由于在spfa初始化的时候默认所有的dist都是inf，因此可以用很多正边去松弛他，但若此时再去跑minMaxflowCost则会导致流量可以变大，但是结果反而变小了，因此在此之前就必须退出得到结果。当然这不用去担心必经点没法跑完，因为在必经点拆点时将其设成-inf，一定满足可以松弛，并且保证松弛后dist<0。所以在流充足的前提下，必经点是一定可以跑完的（除非由于第一个限制因素（流cap不足）就卡掉）。 拆点方式可以学一手（二维数组直接记录）。 （网络流板子from kuangbin） 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
#include<bits/stdc++.h>
using namespace std;
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
template <class T>
struct rbtree: tree<T,null_type,less<T>, rb_tree_tag,tree_order_statistics_node_update>{};
#define int long long
#define IN freopen("in.txt", "r", stdin);
#define endl '\n'
#define mp make_pair
#define pb push_back
#define lowb lower_bound
#define eb emplace_back
#define fi first
#define se second
#define all(x) x.begin(),x.end()
#define sz(x) (int)x.size()
#define mem0(a) memset((a), 0, sizeof(a))
#define mem(a, b) memset((a), (b), sizeof(a))
typedef unsigned long long ull;
typedef long long ll;
typedef vector<int> VI;
typedef vector<ll> VL;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int maxn = 1e5;
const int maxm = 1e7;
const int inf = 0x3f3f3f3f;
const int INF = 0x3f3f3f3f3f3f3f3f;
struct Edge{
    int to, next, cap, flow, cost;
}e[maxm];
int head[maxn], tol;
int pre[maxn], dis[maxn];
bool vis[maxn];
int N;
void init(int n){
    N = n;
    tol = 0;
    memset(head, -1, sizeof(head));
}
void addedge(int u, int v, int cap, int cost){
    e[tol].to = v;
    e[tol].cap = cap;
    e[tol].cost = cost;
    e[tol].flow = 0;
    e[tol].next = head[u];
    head[u] = tol++;
    e[tol].to = u;
    e[tol].cap = 0;
    e[tol].cost = -cost;
    e[tol].flow = 0;
    e[tol].next = head[v];
    head[v] = tol++;
}
bool spfa(int s, int t){
    queue<int> q;
    for(int i = 0; i < N; i++){
        dis[i] = INF;
        vis[i] = false;
        pre[i] = -1;
    }
    dis[s] = 0;
    vis[s] = true;
    q.push(s);
    while (!q.empty()){
        int u = q.front();
        q.pop();
        vis[u] = false;
        for(int i = head[u]; i != -1; i = e[i].next){
            int v = e[i].to;
            if(e[i].cap > e[i].flow && dis[v]>dis[u]+e[i].cost){
                dis[v] = dis[u] + e[i].cost;
                pre[v] = i;
                if(!vis[v]){
                    vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
    if(dis[t]>=0)return false;//1！！！
    return pre[t] != -1;
}
int minCostMaxflow(int s, int t, int &cost){
    int flow = 0;
    cost = 0;
    while(spfa(s, t)){
        int Min = inf;
        for(int i = pre[t]; i != -1; i = pre[e[i^1].to]){
            if(Min > e[i].cap - e[i].flow)
                Min = e[i].cap - e[i].flow;
        }
        for(int i = pre[t]; i != -1; i = pre[e[i^1].to]){
            e[i].flow += Min;
            e[i^1].flow -= Min;
            cost += e[i].cost*Min;
        }
        flow += Min;
    }
    return flow;
}
char a[100][100];
int b[100][100];
int now[100][100];
int fa[100][100];
int dx[4] = {-1, 0, 0, 1};
int dy[4] = {0, 1, -1, 0};
int32_t main(){
    IOS;
    //IN;
    int t; cin>>t;
    while (t--){
        int cnt = 0;
        int S = cnt++, T = cnt++;
        int n, m; cin>>n>>m;
        int c = 0;
        for(int i = 0; i < n; i++)for(int j = 0; j < m; j++){now[i][j] = cnt++, fa[i][j] = cnt++;}
        init(cnt);
        for(int i = 0; i < n; i++) cin>>a[i];
        for(int i = 0; i < n; i++)for(int j = 0; j < m; j++) cin>>b[i][j];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(a[i][j] == '*')continue;
                if(a[i][j] == '#'){
                    c++;
                    addedge(now[i][j], fa[i][j], 1, -b[i][j]-inf);//2！！！
                }else if(a[i][j] == '.'){
                    addedge(now[i][j], fa[i][j], 1, -b[i][j]);
                }
                if((i+j)&1){
                    addedge(S, now[i][j], 1, 0);
                    for(int z = 0; z < 4; z++){
                        int xx = dx[z]+i, yy = dy[z]+j;
                        if(xx >= 0 && yy >= 0 && xx < n && yy < m && a[xx][yy]!='*'){
                            addedge(fa[i][j], now[xx][yy], 1, 0);
                        }
                    }
                }else addedge(fa[i][j], T, 1, 0);
            }
        }
        ll ans = 0;
        minCostMaxflow(S, T, ans);
        ans += c*inf;
        if(abs(ans) >= n*m*10000){//3！！！
            cout<<"no solution"<<endl;
        }else cout<<-ans<<endl;
    }
    return 0;
}

F. Lady Layton with Math

反演过程
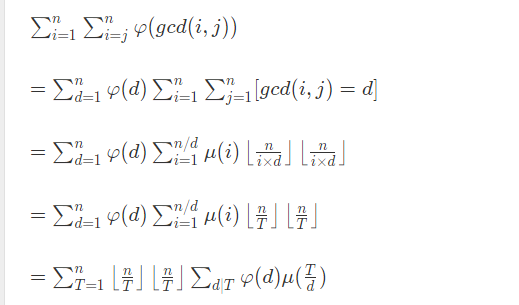
第一个等号的地方不知道，剩下都是套路的操作，可以学的是在maxn~1e9范围内mu，phi的求法。
反演式子是很重要很重要的操作，这方面能力还远远不够，寒假时候要尽量做一些题，这些东西真的是知道就知道，不知道的话就是死活也不会了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
/****************************************************************
# @Author:      miniLCT
# @DateTime:    2019-12-09 08:35:54
# @Description: You build it. You run it 
# @More: Once lots of AC, try Brute-force,dynamic programming 
****************************************************************/
#include<bits/stdc++.h>
using namespace std;
#define close std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define eps 1e-8
#define int long long 
typedef long long ll;
const int maxn = 1e6+10;
const int INF = 1e9;
const ll linf = 0x3f3f3f3f3f3f3f3f;
const double PI = acos(-1.0);
ll mod = 1e9+7;
int prime[maxn], mu[maxn], phi[maxn], v[maxn];
void sieve(){
    int cnt = 0;
    phi[1] = mu[1] = 1;
    for(int i = 2; i < maxn; i++){
        if(!v[i]){  //质数
            prime[cnt++] = i;
            phi[i] = i-1;
            mu[i] = -1;
        }
        for(int j = 0; j < cnt; j++){
            int k = i * prime[j];
            if(k >= maxn)break;
            v[k] = 1;
            if(i % prime[j] == 0){
                phi[k] = phi[i] * prime[j]; // Euler函数性质
                mu[k] = 0;
                break;
            }else {
                phi[k] = phi[i] * (prime[j] - 1);
                mu[k] = -mu[i];
            }
        }
    }
    for(int i = 1; i < maxn; i++){  //在1~maxn这个就是前缀和了
        phi[i] = phi[i-1] + phi[i];
        mu[i] = mu[i-1] + mu[i];
    }
}
map<int , int >musum;
map<int , int >phisum;
/*int get_mu(int x){
    if(x < maxn) return mu[x];
    if(musum[x])return musum[x];
    int ans = 1;
    for(int l = 2, r; l <= x;l = r+1){
        r = x/(x/l);
        ans -= 1ll*(r-l+1)*get_mu(x/l);
    }
    return musum[x] = ans;
}*/
int get_phi(int x){
    if(x < maxn) return phi[x] % mod;
    if(phisum[x]) return phisum[x] % mod;
    int ans;
    if(x & 1){
        ans = (x+1) / 2 % mod * x % mod;
    }else {
        ans = x/2%mod*(x+1)%mod;
    }
    for(int l = 2,r;l <= x;l = r + 1){
        r = x/(x/l);
        ans = (ans - (r-l+1) % mod*get_phi(x/l) % mod);
        ans = (ans + mod) % mod;
    }
    return phisum[x] = ans;
}
int32_t main()
{
    int t ;
    cin >> t;
    sieve();
    while(t--){
        int n ;
        cin >> n;
        int ans = 0;
        for(int l = 1, r ; l <= n; l = r+1){
            r = n/(n/l);
            ans += (get_phi(r)-get_phi(l-1)+mod)%mod*(get_phi(n/l)*2-1+mod)%mod;
            ans = (ans + mod) % mod;
        }
        cout << ans << endl;
    }
}
/***************************************************************************
 *stuff you should look for
 *int overflow, array bounds
 *special cases (n=1?), set tle
 *do smth instead of nothing and stay organized
***************************************************************************/

D.雷顿女士与分队（hard version）

挂下这个DP。。。
还是挺常见的转移

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
const int inf = 0x3f3f3f3f;
int a[N];
int dp[N];
int main(){
    //freopen("in.txt", "r", stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t; cin>>t;
    while(t--){
        int n, k; cin>>n>>k;
        for(int i = 1; i <= n; i++) dp[i] = 0, cin>>a[i];
        for(int i = 1; i <= k-1; i++) dp[i] = inf;
        sort(a+1, a+1+n);
        for(int i = 1; i <= n; i++){
            if(i%k==0) dp[i] = dp[i-k]+a[i]-a[i-k+1];
            else{
                if(i > k) dp[i] = min(dp[i-1]+a[i]-a[i-1], dp[i-k]+a[i]-a[i-k+1]);
            }
        }
        cout<<dp[n]<<endl;
    }
    return 0;
}

-------------本文结束感谢您的阅读-------------