序论(杂论)
心血来潮想整理一下。
Fibonacci 还是很著名的 oeis A000045
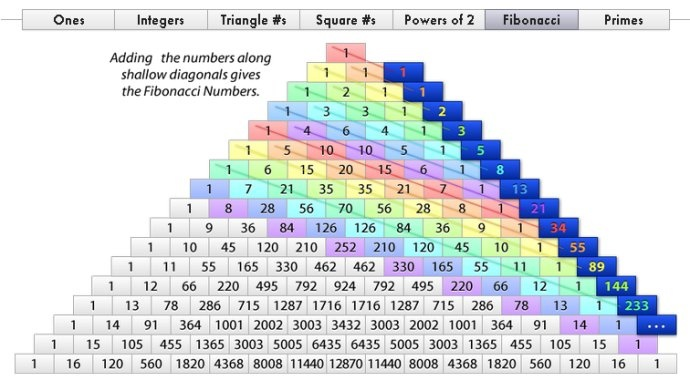
斐波那契数与三角形关系
表达式
- 初等代数解法 略
- 线性代数解法 暂时略
- 数论解法 暂时略
- 组合数解法 暂时略
- 近似值解法 暂时略
- 计算机 :矩阵快速幂优化
这个由于写mathjax本地可以之后部署可能还会有锅就很懒就不想写一大堆式子。之前也遇到过一部分用过这个的题目,贴一下矩阵快速幂板子吧。用矩阵快速幂一定一定一定要想清楚,开数组啊,清零啊什么的。一些性质
- 这里的前提是$f1 = f_2 = 1,f{n+2} = f{n+1}+f{n} \quad(n\ge 1)$
- $F{m+n}=F{m-1} \cdot Fn+F_m \cdot F{n+1}$
- 上式令$m=n$,得到$F{2n} = F_n(F{n+1}+F_{n-1})$
- 由上 归纳证明可得,$\mathsf{\forall} k \in \mathbb{N}, \quad Fn | F{nk}$
- $F1+F_3+\dots +F{2n-1} = F{2n},F_2 + F_4 + \dots + F{2n} = F_{2n + 1} - 1$
- $\sum{i=1}^n F_i = F{n+2} - 1$
- $\sum{i=1}^n F_i^2 = F_n \cdot F{n+1}$
- $\sum{i=1}^n k\cdot F_k = n\cdot f{n+2}-f_{n+3}+2, n\ge 1$
- 卡西尼性质(Cassini’s identity) : $Fn^2=(-1)^{n-1} + F{n-1} \cdot F_{n+1}$
- $Fn^2+F{n-1}^2 = F_{2n-1}$
- $gcd(Fa, F_b)=F{gcd(a, b)}$
- 齐肯多夫定理:任何正整数都可以表示成若干个不连续的斐波那契数之和。利用贪心的算法可以每回都找到最大可能的斐波那契数。
- 以斐波那契数列相邻两项作为输入会使欧几里德算法达到最坏复杂度
- 任意取连续的k项,其$\sum$不会出现在数列中
- 在Fibonacci数列中,每一项模K后(K为正整数)所形成的数列一定会循环,下面会讨论一下这个性质。
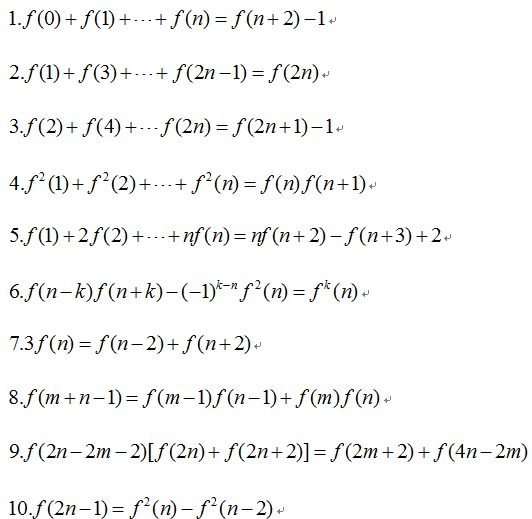
相关数列:lucas数列,卢卡斯数列和斐波那契数列的一些关系,组合数学上的一些恒等式 反费波那西数列,巴都万数列,佩尔数列 等等 在此就不一一赘述。
模意义下的周期性
定义:
对于任意整数$n$,数列{$f_i (mod\quad n)$}为周期数列,皮萨诺周期$\pi(n)$记作该数列的周期,例如模3的斐波那契数列前若干项是$0, 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, 2, 2, 1, 0…………$
oeisA082115 这一数列的周期是8,即$\pi(3)=8$
性质:
- 有趣的一个点是除了$\pi(2) = 3$ 以外,皮萨诺周期都是偶数。
- 模$n$意义下的Pisano numbers总是不超过$6n$,并且只有在$n=2 \times 5^k$时猜取得等号。
模 $n$ 周期(皮萨诺周期)
$\pi(p^k) = p^{k-1} \pi(p)$
$\pi(nm) = lcm(\pi(n), \pi(m)), \forall n \perp m$
$\pi(2)=3, \pi(3)=8, \pi(5)=20$
$\forall p \equiv \pm 1\pmod {10}, \pi(p)|p-1$
$\forall p \equiv \pm 2\pmod {5}, \pi(p)|2p+2$
求法
problem 计算$F(n) mod \ P \quad(n\le10^{30000000},P\le10^{12})$
论文 The Period of the Fibonacci Sequence Modulo j
中文证明的博客 好像前置技能是会二次剩余。
以下是我的理解:求F mod n的循环节长度
step1: 把n进行素因子分解,$n = p_1^{a_1}\cdot p_2^{a_2}…p_k^{a_k}$
step2: 分别计算 F 数模每个$P_m$的循环节长度,假设长度分别为$x_1,x_2,…x_k$。
step3: 那么 F 模n的循环节长度为$L = lcm(x_1,x_2…x_k)$
如此,便可求出循环节长度。那么第二步是关键,如何求 F 模 $p_m$的循环节长度。
这里用了个定理, F 模数字$p_m$的最小循环节长度等于$\pi(p)\times p^{m-1}$,其中$\pi(p)$表示 F 模素数 p 的最小循环节长度。如此只要求出$\pi(p)$.
用以下定理便可以求出$\pi(p)$:
如果5是模p的二次剩余($p\equiv\pm 1(mod \ 5)$),那么循环节长度是$p-1$的因子,否则($p\equiv\pm 2 (mod \ 5)$)是$2(p+1)$的因子。对于小于等于5的素数。$\pi(2)=3, \pi(3)=8, \pi(5)=20$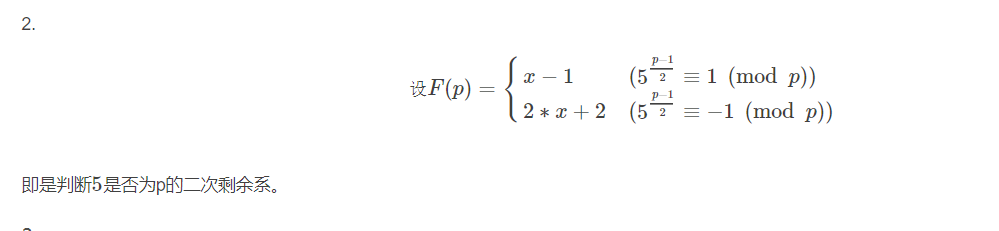
一些代码:
java求小于1000项的f(from claris)连注释都打上了qwq
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18import java.math.BigInteger;
import java.util.Scanner;
public class Main{
public static void main(String[] args){
BigInteger f[] = new BigInteger[1005];//数组用法和c++类似
//二维数组BigInteger[][] f = new BigInteger[1005][1005]
f[1] = BigInteger.valueOf(1);f[2] = BigInteger.valueOf(1);
for (int i=3;i<=1000;i++)f[i]=f[i-2].add(f[i-1]);
Scanner input = new Scanner(System.in);
int n , t;
//用for(...;t−−;)替代会报错,因为要求第二个表达式必须返回bool
for(t=input.nextInt();t>0;t--){
n=input.nextInt();
System.out.println(f[n]);
}
}
}快速倍增法
由等式
于是可以通过这样的方法快速计算两个相邻的斐波那契数(常数比矩乘小)。代码如下,返回值是一个二元组$(Fn,F{n+1})$。1
2
3
4
5
6
7
8
9
10
11//from oi-wiki
pair<int, int> fib(int n) {
if (n == 0) return {0, 1};
auto p = fib(n >> 1);
int c = p.first * (2 * p.second - p.first);
int d = p.first * p.first + p.second * p.second;
if (n & 1)
return {d, c + d};
else
return {c, d};
}
- 求循环节长度 51nod1195
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94//others
typedef long long ll;
using namespace std;
int T,n;
const ll INF=0x3f3f3f3f3f3f3f3f;
tr1::unordered_map<ll,ll>S;
inline ll power(ll a,ll b,ll mod){
int rs=1;a=a%mod;
for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)rs=1ll*rs*a%mod;
return rs;
}
inline ll gcd(ll x,ll y){return y?(gcd(y,x%y)):x;}
typedef pair<int,int> pii;
namespace SP1{
vector<pii>fac;
ll nowlen,M;
inline void mul(ll *a,ll *b,ll mod){
unsigned long long bd=a[0]*b[0],bc=a[0]*b[1],ad=a[1]*b[0],ac=a[1]*b[1];
a[1]=(bc+ad+ac)%mod,a[0]=(bd+ac)%mod;
}
inline void power_p(ll *a,ll b,ll mod){
ll c[2]={1,0};
for(;b;b>>=1,mul(a,a,mod))
if(b&1)mul(c,a,mod);
a[0]=c[0];a[1]=c[1];
}
inline bool check(ll sum){
ll b[2]={0,1};
power_p(b,sum,M);
return b[1]==0&&b[0]==1;
}
inline void dfs(int pos,ll sum){
if(pos==fac.size()){
(sum!=1&&check(sum))?(nowlen=min(nowlen,sum)):0;
return;
}
ll rs=1;
for(int i=0;i<=fac[pos].SD;++i){
dfs(pos+1,sum*rs);
rs*=fac[pos].FT;
}
}
inline ll getlen(ll x){
if(x==2)return 3;
if(x==3)return 8;
if(x==5)return 20;
if(S.find(x)!=S.end())return S[x];
ll base=(power(5,(x-1)/2,x)==1)?(x-1):(2*x+2);
fac.clear();nowlen=INF;M=x;
for(int i=2;i*i<=base;++i){
if(!(base%i)){
pii t=MP(i,0);
while(!(base%i))base/=i,++t.SD;
fac.PB(t);
}
}
if(base!=1)fac.PB(MP(base,1));
dfs(0,1);return S[x]=nowlen;
}
}
vector<pii>fac;
ll ans;
inline void solve(int n){
if(n==1){puts("1");return;}
fac.clear();
for(int i=2;i*i<=n;i++){
if(!(n%i)){
pii t=MP(i,0);
while(!(n%i))n/=i,++t.SD;
fac.PB(t);
}
}
if(n!=1)fac.PB(MP(n,1));
ans=1;
for(int i=0;i<fac.size();++i){
ll l=SP1::getlen(fac[i].FT);
l=l*power(fac[i].first,fac[i].second-1,INF);
ans=(ans*l)/gcd(ans,l);
}
printf("%llu\n",ans);
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d",&n);
solve(n);
}
}