擅长用概率为零的事件使用条件概率。
具体数学第2版。坑大无比,能填多少是多少
习题选取为部分我感兴趣的并且能基本弄懂的。
递归问题
河内塔
The Tower of Hanoi
$T(n) = 2T(n-1)+1$
$T(0) = 0$
$T(1) = 1$ …………
$\Rightarrow T(n) = 2^n-1$
来个大一上写的代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
using namespace std;
int num;
void move(int x, char a , char b , char c){ // a起始座,b辅助座,c终点座
if(x == 1) printf("%c --> %c\n", a, c); // 盘子数量为1时候
else{
move(x-1, a , c , b); //先将前x-1个盘借助c放到b上
printf("%c --> %c\n", a, c); // 将最后一个盘子放到目标座
move(x-1 , b , a , c);//将前x-1个盘借助a放到c上
}
}
void Hanoi(int x){
move(x , 'A', 'B', 'C');
}
int main()
{
cout << "请输入盘的数量:"<<endl;
cin >> num;
Hanoi(num);
}
平面上的直线
Lines in The Plane
Part1
“What is the maximum number Ln of regions defined by n lines in the plane?”
平面上 $n$ 条直线所界定的区域的最大个数 $L_n$ 是多少。
画图观察可知,$L_o = 1, L_1 = 2, L_2 = 4,L_3 = 7。$
对第 $n$ 条线的构造,由已有 $n-1$ 条直线,所以第n条直线最多和已有直线产生 $n-1$ 个交点,所以增加的平面数量的最大值为 $n$,由此一个可行解,它是充分的 $Ln \le L{n-1} + n (n>0)$
接下来试图说明它的必要性:只要把第 $ n$ 条直线放在与前$n-1$ 条都不相交的方向,那么第n条直线必和前n-1条直线各有一个交点。又因为 $L{n-1}$ 为最大值,所以保证了前 $n-1$ 条直线产生的 $n-2$ 个交点互异,可以做到第 $n$ 条直线产生的 $n-1$ 个新交点彼此互异,且和前$ n-2 $个交点也互异。由此 $Ln \ge L{n-1} + n (n>0)$。
由此,有递归式:
Part2
折线代替直线,求形成区域的$MAX$
HDU折线分割平面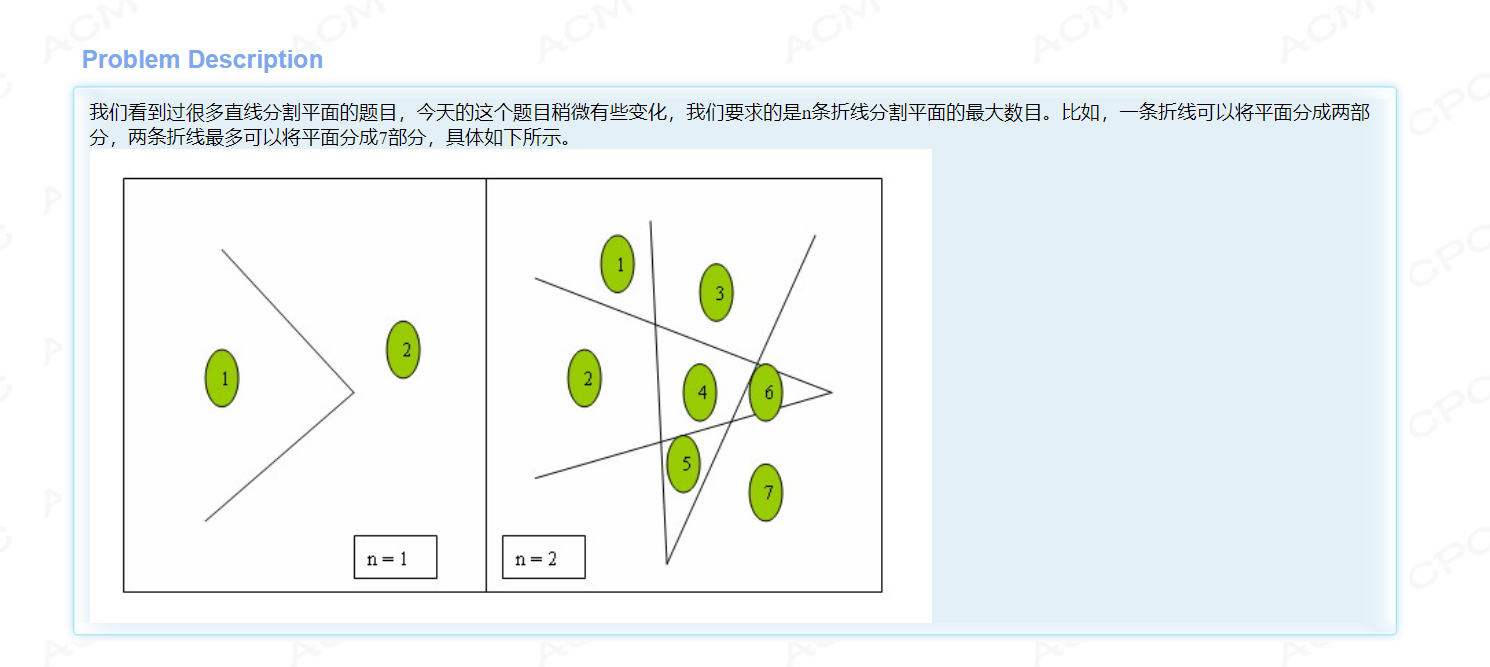
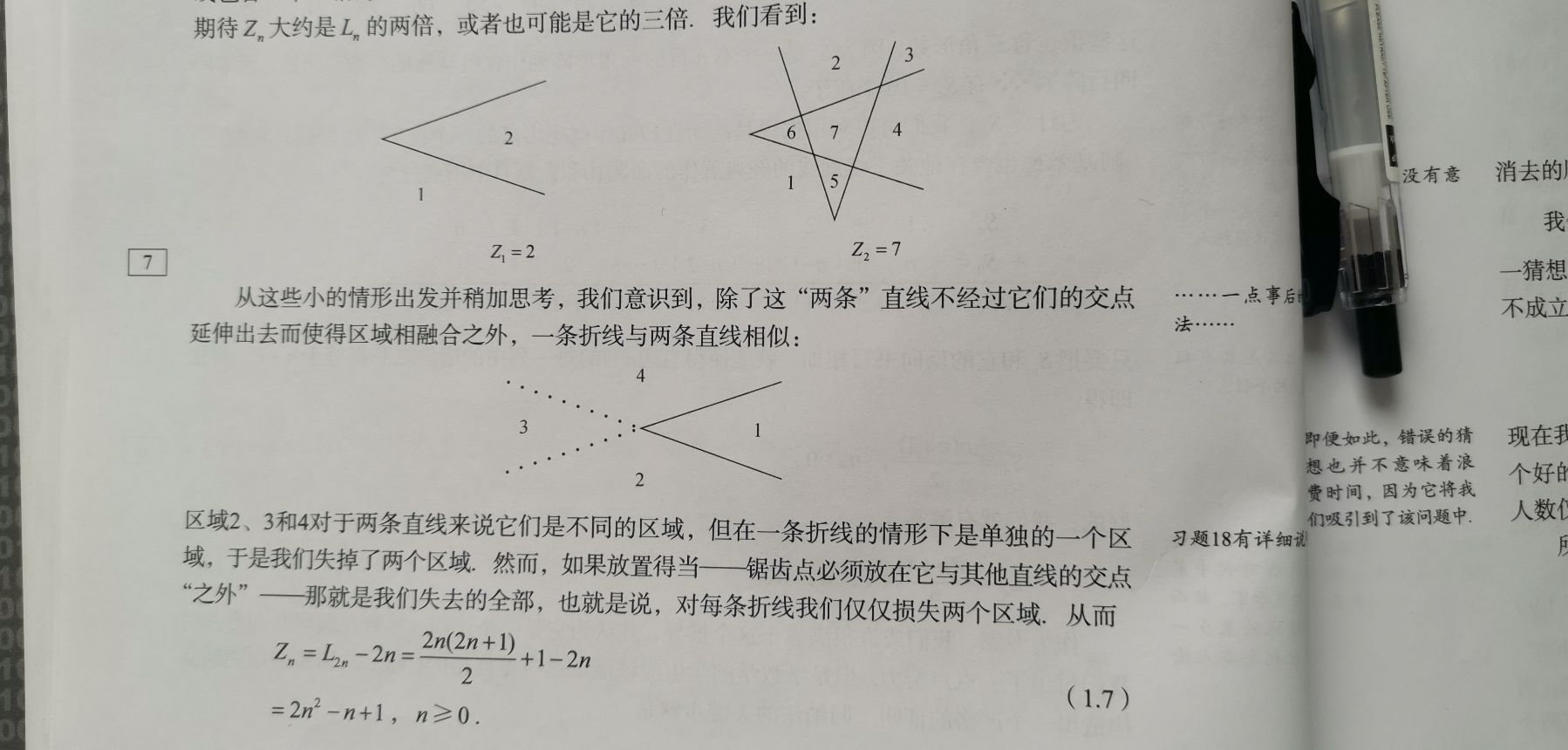
将折线看作直线处理,考虑到折线外形成的区域,发现每个折线失去了两个区域。
容易得到递归式:
约瑟夫问题
The Josephus Problem
Base
基于从围成标有记号 $1$ 到 $n$ 的圆圈的$n$ 个人开始,每隔一个 删去一个人。
显然:偶数的在第一轮就被删完了。这没多大用
以下用 $J(n)$ 表示 $n$ 个人时候,幸存者的编号。
对小数进行模拟表发现
感觉发现了规律
可以证明上式是对的,此处略。
以下说明另一个结论,考虑$n$,$J(n)$的以2为基数的表示,假设$n$的二进制展开式为$n = (bmb{m-1}…b1b_0)_2 \quad \Leftrightarrow \quad n = b_m2^m+b{m-1}2^{m-1}+……+b12+b_0$
推得$J((b_mb{m-1}…b1b_0)_2 ) = (b{m-1}…b_1b_0b_m)_2)$ $\quad n$左循环一位得到 $J(n)$
- 重复运用 $J$ 的性质会得到一系列递减的值。最终达到一个不动点。此不动点有$J(n) = n = 2^{v(n)}-1$ ,$\quad v(n)$是$n$的二进制表示中 $1$ 的个数。例如有$v(13) = 3$
Extension
引入常数$\alpha,\beta,\gamma $。
观察到我们可以将 $f(n)$ 表示为以下形式:
可以证明得到$A(n)=2^m,B(n)=2^m-1-l,C(n) = l \quad n=2^m+l,0\le l\lt2^m(n\ge1)$
联系之前约瑟夫递归式有个写成二进制的解,$J((bmb{m-1}…b1b_0)_2 )= (b{m-1}…b_1b_0b_m)_2)$,现在考虑推广的有无这样特殊的解。
不妨令$\beta_0=\beta,\beta_1=\gamma$,这样递归式写成$f(1)=\alpha,f(2n+j)=2f(n)+\beta_j,\quad j=0,1,n\ge1$
这个递归式按照二进制展开得到
现在进一步推广,不仅仅限于二进制表示,允许任何的数字(不仅限于0,1),那么,上述的推导告诉我们
把$100$带进去很快就能验证到这是正确的。(偷懒以下就不打了)
循环移位的性质!
好,接下来对于一般的递归式,
基数是 $d$ 的数着手,产生的值是用基数 $c$ 表示。给出了如下解: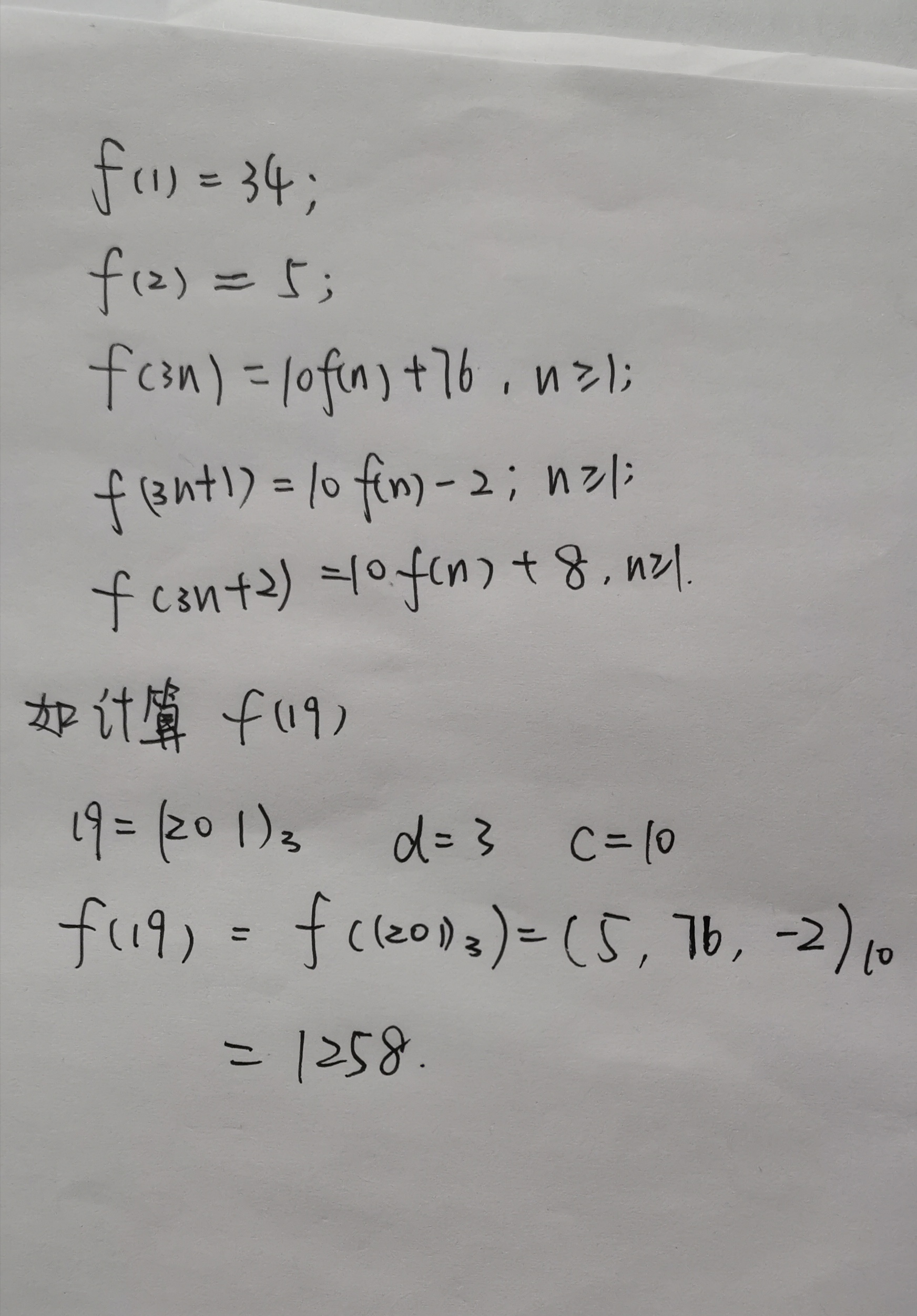
不怎么相关的阅读资料
习题选取
和式
记号
Notation
$\sum$ 大写的($\sigma$)
和式和递归式
Sums And Recurrences
和式的处理
Manipulation of Sums
多重和式
Multiple Sums
一般性的方法
有限微积分和无限微积分
无限和式
习题选取
整值函数
底和顶
底和顶的应用
底和顶的递归式
mod:二元运算
底和顶的和式
习题选取
数论
整除性
素数
素数的例子
阶乘的因子
互素
mod:同余关系
独立剩余
进一步的应用
$\varphi$函数和$\mu$的应用
习题选取
二项式系数
基本恒等式
基本联系
处理的技巧
生成函数
超几何函数
超几何变换
部分超几何和式
机械求和法
习题选取
特殊的数
斯特林数
欧拉数
调和数
调和求和数
伯努利数
斐波那契数
连项式
习题选取
生成函数
多米诺理论与换零线
基本策略
解递归式
特殊的生成函数
卷积
指数生成函数
狄利克雷生成函数
习题选取
离散概率
定义
均值与方差
概率生成函数
抛掷硬币
散列法
习题选取
渐进式
量的等级
大$O$记号
$O$运算规则
两个渐进技巧
欧拉求和公式
最后的求和法
习题选取
感想
“有两种推广,一种没有什么价值,另一种则是有价值的。没什么思想,仅凭唬人的专门术语做推广是很容易做到的。颇为困难的是从若干好的素材中提取除一份精致凝练的精品。” ——波利亚