dp计划1

你能优化来我的人生吗？

已完成？/50

CF446A - DZY Loves Sequences

Description

给一个长度为 $n$ 的序列，最多可以修改一个位置的数，求最长连续上升子序列。

Solution

当 $a{i+1} > a{i-1}+2$ 时，改变 $a_i$ 的值来使前后两段合并，反之，分别考虑$a_i$左边那段最长的和右边那段最长的。

Code

const int N = 1e6+100;
int a[N], dp[N], l[N], r[N];
int main()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
    }
    dp[1] = 1;
    for(int i= 2; i <= n; i++){
        if(a[i] > a[i-1]) dp[i] = dp[i-1] + 1;
        else dp[i] = 1;
    }
    r[n] = n;
    for(int i = n-1; i >= 1; i--){
        if(a[i] < a[i+1]) r[i] = r[i+1];
        else r[i] = i;
    }
    int ans = 0;
    for(int i = 1; i <= n; i++){
        int tp = dp[i-1] + 1;
        if(a[i+1] >= a[i-1] + 2){
            ans = max(ans , tp + r[i+1] - i);
        }else {
            ans = max({ans, tp, r[i+1] - i + 1});
        }
    }
    cout << ans << endl;
    return 0;
}

CF4D - Mysterious Present

Description

给出n个信封，这n个信封有长和宽，给出卡片的尺寸，求取能够装入卡片的最长的序列，序列满足后一个的长和宽一定大于前一个（套娃），求最长的这个序列的长度。

Solution

$dp[i] = \max_{j=0}^{j-1} { dp[j]+1 } , { a[j].w < a[i].w \ \&\& \ a[j].h < a[i].h }$

记个pre倒序输出答案。

Code

const int N = 1e6+100;
struct node
{
    int w , h , id;
    friend int operator < (const node &a , const node &b){
        if(a.w == b.w) return a.h < b.h;
        else return a.w < b.w;
    }
    /* data */
}a[N];
int main()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int n , h , w;
    cin >> n >> w >> h;
    for(int i = 1; i <= n; i++){
        cin >> a[i].w >> a[i].h;
        a[i].id = i;
    }
    sort(a+1, a+1+n);
    vector<int> dp(n+10), pre(n+10);
    for(int i = 1; i <= n; i++){
        if(a[i].h <= h || a[i].w <= w) continue;
        dp[i] = 1;
        for(int j = 1; j < i; j++){
            if(a[i].w > a[j].w and a[i].h > a[j].h) {
                if(dp[i] < dp[j] + 1){
                    dp[i] = dp[j]+1;
                    pre[i] = j;
                }
            }
        }
    }
    int mx = 0, pos = 0;
    for(int i = 1; i <= n; i++){
        if(mx < dp[i]) {
            mx = dp[i];
            pos = i;
        }
    }
    function<void (int )> dfs = [&](int x){
        if(!x) return ;
        dfs(pre[x]);
        cout << a[x].id << ' ';
    };
    cout << mx << endl;
    dfs(pos);
    return 0;
}

10
10 11 12 1 2 3 14 7 15 16

串

Description

长度不超过n，且包含子序列“us”的、只由小写字母构成的字符串有多少个？答案对10^9+7 取模。
所谓子序列，指一个字符串删除部分字符（也可以不删）得到的字符串。
例如，”unoacscc”包含子序列”us”，但”scscucu”则不包含子序列”us”

Solution

dp[i][0]无u

dp[i][1]有u无s

dp[i][2]有us

考虑状态转移。
$dp[i][0] = 25*dp[i-1][0]$ 最后有25种选择

$dp[i][1] = 25dp[i-1][1]25+dp[i][0]$前面有u的随意加，无u的加u

$dp[i][2] = dp[i-1][1]+dp[i-1][2]*26$ 有u的串最后一位加上s，加上之前us的串随意加

Code

int dp[maxn][3];
// dp[i][0]无u
// dp[i][1]有u无s
// dp[i][2]有us
int32_t main()
{
    int n, ans = 0; cin >> n;
    dp[1][0]=25,dp[1][1]=1,dp[1][2]=0;
    for(int i = 2; i <= n; i++){
        add(dp[i][0], dp[i-1][0] * 25 % mod);
        add(dp[i][1], (dp[i-1][1]*25+dp[i-1][0])%mod);
        add(dp[i][2],(dp[i-1][1]+dp[i-1][2]*26)%mod);
        add(ans , dp[i][2]);
    }cout << ans << endl;
    return 0;
}

cf#544 div.3-E. K Balanced Teams

Description

Solution

Code

// She is Pretty pretty!
#include <bits/stdc++.h>
using namespace std;


#define ll long long
#define ff first
#define ss second
#define mp make_pair
#define pb push_back

const int N = 5005;
int n, k, a[N], dp[N][N];
int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a + 1, a + n + 1);
    int zz = n;
    for (int i = n; i >= 1; i--) {
        while (a[zz] > a[i] + 5) zz--;
        for (int j = 1; j <= k; j++) {
            dp[i][j] = max(dp[i + 1][j], dp[zz + 1][j - 1] + (zz + 1 - i));
        }
    }
    cout << dp[1][k];
    return 0;
}

美团2017年CodeM大赛-初赛A轮-合并回文子串

Description

$a,b$ 两个串保持字符顺序不变组合成字符串$c$ ,求字符串 $c$ 可能形成的最长回文子串的长度。

Solution

区间dp。
官方题解
设 $f[l1][r1][l2][r2]$ 表示$A[l1] \sim A[r1]$ 和 $B[l2] \sim B[r2]$ 是否能合并成一个回文串。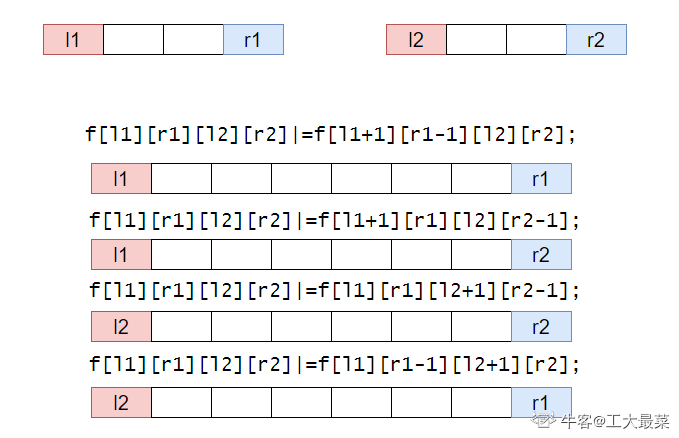
from：牛客 https://blog.nowcoder.net/n/51d6684184b64b1399859ad5a22cbb5f
所以dp转移如图所示，

$dp[l1][r1][l2][r2] |= dp[l1+1][r1-1][l2][r2];$
$dp[l1][r1][l2][r2] |= dp[l1+1][r1][l2][r2-1];$
$dp[l1][r1][l2][r2] |= dp[l1][r1][l2+1][r2-1];$
$dp[l1][r1][l2][r2] |= dp[l1][r1-1][l2+1][r2];$
需要注意的是，当两个串选出的字符只有一个时候，认为是可以构成回文串的。（边界条件）

Complexity: $O(T\times n^4)$

Code

char a[maxn], b[maxn];
int dp[maxn][maxn][maxn][maxn];
//区间dp
int main() {
    CASET {
        scanf("%s%s", a + 1, b + 1);
        int lena = strlen(a + 1);
        int lenb = strlen(b + 1);
        int ans = 0;
        memset(dp , 0 , sizeof dp);
        for (int i = 0; i <= lena; i++) {      // a的长度
            for (int j = 0; j <= lenb; j++) {  // b的长度
                for (int l1 = 1, r1 = l1 + i - 1; r1 <= lena; l1++, r1++) { //枚举a的起点终点部分
                    for (int l2 = 1, r2 = l2 + j - 1; r2 <= lenb; l2++, r2++) { //枚举b的起点终点部分
                        if (i + j <= 1) {
                            dp[l1][r1][l2][r2] = 1;
                        } else {
                            if(a[l1]==a[r1]&&r1>0) dp[l1][r1][l2][r2] |= dp[l1+1][r1-1][l2][r2];
                            if(a[l1]==b[r2]&&r2>0) dp[l1][r1][l2][r2] |= dp[l1+1][r1][l2][r2-1];
                            if(b[l2]==b[r2]&&r2>0) dp[l1][r1][l2][r2] |= dp[l1][r1][l2+1][r2-1];
                            if(b[l2]==a[r1]&&r1>0) dp[l1][r1][l2][r2] |= dp[l1][r1-1][l2+1][r2];
                        }
                        if (dp[l1][r1][l2][r2])
                            ans = max(ans, r1 - l1 + r2 - l2 + 2);
                    }
                }
            }
        }
        cout << ans << endl;
    }
}

2018年长沙理工大学程序设计竞赛-数学考试

Description

给定一个序列，选取两个不相交的长度为 k 的区间求和， MAX 这个和。

Solution

nowcoder官方题解
前缀和+暴力dp
对序列求前缀和得到 $sum$ 。设 $dp1_i$表示位置$i$ 之前最大的区间和，$dp2_i$表示位置$i$之后最大区间和。线性更新一下就OK了。

Complexity: $O(T\times n)$

Code

int a[maxn], dp1[maxn], dp2[maxn], sum[maxn], n, k, ans;
int32_t main() {
    close;
    CASET {
        cin >> n >> k;
        memset(dp1, 0xcf, sizeof dp1);
        memset(dp2, 0xcf, sizeof dp1);
        ans = -linf;
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
            sum[i] = sum[i - 1] + a[i];
        }
        // dp1 之前一段的max  dp2 之后的一段
        for (int i = k; i <= n - k; i++) {
            dp1[i] = max(sum[i] - sum[i - k], dp1[i - 1]);
        }
        for (int i = n - k + 1; i >= k + 1; i--) {
            dp2[i] = max(sum[i + k - 1] - sum[i - 1], dp2[i + 1]);
        }
        for (int i = k; i <= n - k; i++) {
            ans = max(ans, dp1[i] + dp2[i + 1]);
        }
        cout << ans << endl;
    }
}

others 线段树：博客

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll sum[422222],a[422222];
struct stree{
    int p,l,r;
    ll ma;
};
stree t[800020];
void build(int p,int l,int r){        //递归建立线段树
    t[p].l=l,t[p].r=r;                //线段树的区间左端点和右端点赋值。
    if(l==r){t[p].ma=a[l];return;}
    int mid=l+r>>1;
    build(p*2,l,mid);                //递归左儿子
    build(p*2+1,mid+1,r);            //递归右儿子
    t[p].ma=max(t[2*p].ma,t[2*p+1].ma);    //区间最大值赋值。
}
ll ask(int p,int l,int r){    //在节点p对应区间找原数组里l到r的最大值
    if(t[p].l>=l&&t[p].r<=r)return t[p].ma;    //若p对应区间被包含在[l,r]区间里，则直接返回。
    int mid=t[p].l+t[p].r>>1;
    ll ma=-1e18;
    if(l<=mid)ma=max(ma,ask(p*2,l,r));    //递归找左节点
    if(r>mid)ma=max(ma,ask(p*2+1,l,r));    //递归找右节点
    return ma;
}
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,k,i,x;
        ll s=0;
        cin>>n>>k;
        for(i=1;i<=n;i++){
            scanf("%d",&x);
            s+=x;
            sum[i]=s;
        }
        for(i=1;i<=n-k+1;i++){
            a[i]=sum[i+k-1]-sum[i-1];
        }
        build(1,1,n-k+1);
        ll ma=-1e18;
        for(i=1;i<=n-2*k+1;i++){
            ma=max(ma,a[i]+ask(1,i+k,n-k+1));
        }
        cout<<ma<<endl;
    }
}

expansion

不限制长度—在一个数列里找两个不相交区间使得他们权值和最大
区间数目变多—找 $m$ 个长度为 $k$ 的不相交区间使得他们的权值和最大 $(1\leq n \leq 5000)$
区间数目变多且不限制长度—找 $m$ 个不相交长度不限的区间使他们的权值和最大 $(1\leq n \leq 5000)$

官方

some ideas:
bonus1: 设 $fi$表示前 $[1,i]$ 的最大子段和， $g_i$表示 $[i,n]$ 的最大子段和。那么有$ans = \mathbb {MAX}{ f_i+g{i+1}}$
bonus2: 设 $f{i,j}$ 表示前 $i$ 个数，分成$j$ 段长度为 $k$ 的连续子段的最大值，那么有转移方程: $f{i,j} = \mathbb{MAX} (f{i-1,j} \ , f{i-k,j-1}+si-s{i-k})$
bonus3: 设$f_{i,j,0/1}$ 表示前 $i$ 个数，分成 $j$ 段，第 $i$个不选/选的最大值，考虑第 $i$ 个是不是新开一段。于是有以下的转移方程。

$\begin{cases} f_{i,j,0}=max(f_{i-1,j,0},f_{i-1,j,1})\\ f_{i,j,1}=max(f_{i-1,j,1},f_{i-1,j-1,1},f_{i-1,j-1,0})+a_i\\ \end{cases}$

Description

Solution

Code

Codeforces Round #635 (Div. 2)-E. Kaavi and Magic Spell

Description：

给定一个长度为 $n$ 的字符串 $S$ 和一个长度为 $m$ 的字符串$T$, 有 $1\le m \le n$,开始有一个空串 $A$, 接下来对 $S$ 串进行 n 次操作：

把 S 的首字符加到 A 的开头
把 S 的首字符加到 A 的结尾
问在操作过程中使得 A 的前 m 个字符为字符串 T 的方案数。认为长度不同或者是操作序列中有某个地方不同是不同情况。

Solution:

区间 $DP$。
不妨假设 $T$ 串为 “asd”
$A$ 串为”asd*(补到与S串等长)”
定义 $dp[l][r]$ 为满足 $\forall \ l \le i \le r, S_i=T_i$能构造出来的操作序列。
假设删除$S_i$往 $A$ 里添加（此时$A$有$i-1$个元素），考虑状态转移方程。
考虑两个东西： $dp[l][r]$和$r-l+1=i$

如果有$S_i=T_l$ 那么就把 $S_i$放到$[l+1,r]$区间的前面，构成$[l,r]$ 即有$dp[l][r]+=dp[l+1][r]$
如果有$S_i=T_r$ 那么就把 $S_i$放到$[l,r-1]$区间的后面，构成$[l,r]$ 即有$dp[l][r]+=dp[l][r-1]$

初始化状态：区间长度为 1 时如果有字符相等那么就会存在$dp[i][i] += dp[i][i-1]$的情况，对于这种情况其实就是单个字符$S_i$在空串基础上前插或后插后成为了符合条件的串之一，实际上应该是$dp[i][i] += 1$，所以我们就预处理一下使$ dp[i][i-1] = 1 $即可。

统计答案：即统计 A 的前缀部分 $ans=\sum_{i=m}^ndp[1][i]$

Code:

// She is Pretty pretty!
const int N = 3100;
const int mod = 998244353;
char s[N], t[N];
ll dp[N][N];
void add(ll &a, int b) {
    a += b;
    if (a >= mod) a -= mod;
}
int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n, m;
    cin >> s + 1 >> t + 1;
    n = strlen(s + 1), m = strlen(t + 1);
    for (int i = 1; i <= n+10; i++) {
        dp[i][i - 1] = 1;
    }
    for (int i = 1, len = 1; i <= n; i++, len++) {
        for (int l = 1;; l++) {
            int r = l + len - 1;
            if(r > n)break;
            if (l > m || s[i] == t[l]) {
                add(dp[l][r], dp[l + 1][r]);
            }
            if (r > m || s[i] == t[r]) {
                add(dp[l][r], dp[l][r - 1]);
            }
        }
    }
    ll ans = 0;
    for (int i = n; i >= m; i--) {
        add(ans, dp[1][i]);
    }
    cout << ans << endl;
    return 0;
}

Description

Solution

Code

EDU59-E. Vasya and Binary String

Description：

给个长度为 $n (n\le100)$ 的 $01$ 串 $s$ ,以及长度为 $n$ 数组 $a$.每次可以选择任意长度 $L$ 的连续子串（要求子串每个字符相同）从原串中去掉，并获得 $a[L]$ 的值。问可能获得的最大值

Solution:

观察数据范围，考虑到用区间 $dp$。
令$dp[ l ][ r ][ k ] $代表的是 $[l, r]$这段区间内，前面有 $k-1$ 个连续的和 $s[l]$ 相同且连续的字符传进来的最大值。
$solve( l, r, k)$ 代表的是处理区间$[L, R]$, 正在处理 $[L, R]$这个区间，前面有$k-1$个连续的和$s[l]$相同且连续的字符。
考虑转移状态方程：
$dp[l][r][k] = a[k] + solve(l+1,r,1)$。在 $l$ 这个位置切断连续字符。
$dp[l][r][k] = solve( l+1, i-1, 1) + solve(i, r, k+1)$ 其中 $s[l] == s[i]$ 加入新的连续字符。

Code:

constexpr int N = 201 + 10;
ll n, a[N], dp[N][N][N];
char s[N];

ll solve(int l, int r, int k) {
    if (l > r) return 0;
    if (l == r) return a[k];
    ll &ret = dp[l][r][k];
    if (ret) return ret;
    ret = a[k] + solve(l + 1, r, 1);
    for (int i = l + 1; i <= r; i++) {
        if (s[i] == s[l]) {
            ret = max(ret, solve(i, r, k + 1) + solve(l + 1, i - 1, 1));
        }
    }
    return ret;
}
int main() {
    close;
    cin >> n >> s + 1;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    cout << solve(1, n, 1);
}

Beautiful Mirrors

Description

魔镜魔镜我美嘛easy版本，一个人问魔镜他美嘛，魔镜会有$p_i$ %d 概率说他美，他美就会开心，否则不开心，回到第一天，求开心的期望天数。

Solution

概率求期望题目
不妨设 dp[i] 表示第i到 n+1 天期望步数。那么有 dp[n+1] = 0
则有：

$\begin{cases} dp_1=1+p_1\cdot dp_2+ (1-p_1)\cdot dp_1 \\ dp_2=1+p_2\cdot dp_3+ (1-p_2)\cdot dp_1 \\ \cdots\\ dp_n=1+p_n\cdot dp_{n+1}+(1-p_n)dp_1 \end{cases}$

求解得到：

$\begin{cases} dp_1=dp_2+\frac{1}{p_1} \\ dp_1=dp_3+\frac{1}{p_2}+\frac{1}{p2\cdot p1} \\ \cdots\\ dp_1=dp_{n+1}+\frac{1}{p_n}+\frac{1}{p_n\cdot p_{n-1}}+\cdots +\frac{1}{p_n\cdot p_{n-1}\cdots p_1} \end{cases}$

推得：
$dp1=\frac{1+p_1+p_1p_2+\cdots p_1p_2\cdots p{n-1}}{p_1p_2\cdots p_n}$

Code

ll dp[maxn], a[maxn], b[maxn];
int main()
{
    ll ans = 0, n, x;
    cin >> n;
    ll inv = get_inv(100,mod);
    for(int i = 1; i <= n; i++){
        cin >> x;
        a[i] = x * inv % mod;
        b[i] = get_inv(a[i], mod);
    }
    for(int i = 1; i <= n; i++){
        dp[i] = (dp[i-1] + 1) * b[i] % mod;
    }
    cout << dp[n] <<endl;
}

Beautiful Mirrors with queries

Description

在上题的基础上，要求的是回到 $u$ 。

Solution

考虑$[L , R], ans = \frac{1+pl+p_lp{l+1}\cdots +(pl\cdots p_r)}{p_lp{l+1}\cdots p_r}$
对于求这个，考虑:
定义 $s_i=p_ip_2\cdots p_i,t_i=p_1+p_1\cdot p_2+\cdots + p_1 p_2\cdots p_i$

维护前缀积和累和
$ans=\frac{A}{B}, A=\frac{t{r-1}-r{l-2}}{s{l-2}}, B=\frac{s_r}{r{l-1}}$

Code

set<ll> S;
int n, q, v[maxn];
int p[maxn], t[maxn], inv[maxn], s[maxn];
int query(int l, int r) {
    if (l == 1) {
        ll A = (t[r - 1] + 1) % mod;
        ll B = s[r] % mod;
        return A * get_inv(B, mod) % mod;
    }
    ll A = (t[r - 1] - t[l - 2] + mod) % mod * get_inv(s[l - 1], mod) % mod;
    ll B = s[r] * get_inv(s[l - 1], mod) % mod;
    // cout << "A == " << A << "  B === " << B << endl;
    return A * get_inv(B, mod) % mod;
}
int32_t main() {
    close;
    cin >> n >> q;
    S.insert(1);
    S.insert(n + 1);
    v[1] = 1;
    int inv100 = get_inv(100, mod);
    for (int i = 1; i <= n; i++) {
        cin >> p[i];
        p[i] = p[i] * inv100 % mod;
    }
    s[0] = 1, t[0] = 0;
    for (int i = 1; i <= n; i++) {
        s[i] = s[i - 1] * p[i] % mod;
        t[i] = (t[i - 1] + s[i]) % mod;
    }
    ll ans = query(1, n);
    for (int i = 0; i < q; i++) {
        int x;
        cin >> x;
        if (v[x]) {
            v[x] = 0;
            S.erase(x);
            auto L = S.lower_bound(x);
            // auto L = lower_bound(ALL(S),x);
            auto R = L;
            L--;
            // ans = (ans + query(*L, *R - 1)) % mod;
            // ans = (ans - query(*L, x - 1) + mod) % mod;
            // ans = (ans - query(x, *R - 1) + mod) % mod;
            add(ans, query(*L, *R - 1));
            dec(ans, query(*L, x - 1));
            dec(ans, query(x, *R - 1));
        } else {
            v[x] = 1;
            // auto L = lower_bound(ALL(S),x);
            auto L = S.lower_bound(x);
            auto R = L;
            L--;
            // ans = (ans - query(*L, *R - 1) + mod) % mod;
            // ans = (ans + query(*L, x - 1)) % mod;
            // ans = (ans + query(x, *R - 1)) % mod;
            dec(ans, query(*L, *R - 1));
            add(ans, query(*L, x - 1));
            add(ans, query(x, *R - 1));
            S.insert(x);
        }
        cout << ans << endl;
    }
}