gym102091 E-How Many Groups 关于dp的两种思考

起因

这道题是在3.28日训练赛时候遇到的。当时情况是三个多小时后开了这题，队友在设计三维dp状态转移，然而wa了。当时我个人再看其他题目，等看这个题目时候，迷迷糊糊的，单单是感觉这个值域提醒的200很有文章。队友写了蛮久也没过，可能是边界没有处理好。

其实之前也是做过这类的题目，但是确实存在不是很熟悉的情况。故思考了很久之后，记录一下这两种方法。

Description

给定一个$n(n\le100)$个元素的数组$A(\forall A_i \in A \ \ \ 1\le A_i \le 200)$，定义了关系：有两个数字$a,b$，当且仅当$|a-b|\le2$时，$a,b$在同一组，求一个最大的分组，输出这个分组的数量。（可以对任意位置的数字进行操作+1，或者-1，一共可以操作两次）。

Solution

显然的一个事情，我们可以把数组从小到大排序，然后有个直观的贪心想法是让下面的尽量往下靠靠，让上面的往下靠靠，然后其实很显然（根据数据范围）就能发现这应该往dp方向靠。（贪心不对！）

解法1：

不放设 $dp[i][j][k]$ 表示到以第 $i$ 个数为结尾的，且第 $i$ 个数改了 $j$ 次，第 $i$ 个数改动值为 $k-1$ 的集合最大值。

考虑状态转移：

首先思考如果 $i$ 改动次数为 $0$ 次的情况：

$\begin{cases} dp[i][0][1]=dp[i-1][0][1] + 1& \text{a[i] - a[i-1] <=2}\\ dp[i][0][1] = 1& \text{others} \end{cases}$

然后考虑

j：1->2
  k:0->2
    先给定初始值的状态dp[i][j][k]=1
    枚举i-1的所有修改状态l:0->2
    ai是a[i]修改后的值，aj是a[i-1]修改后的值。
    考虑状态转移：
    第一种是第i个数不修改，dp[i][j][1]直接由dp[i-1][j][l]转移得到
    第二种是第i个数修改，dp[i][j][0|2]有dp[i-1][j-1][l]转移得到

注意在dp过程中不断更新ans

此外特别要注意要使冗余状态不会对结果产生影响：冗余状态的初始值必须为0，这样从冗余态推导到可行态才会变成1 （冗余态不要被赋初值为1即可）

所以一开始不可以将dp数组初始化为0

解法2：

按照值域利用滚动数组记录+1，-1的情况。滚动的原因是，上一个数字如果是拿来减的，那么在本次更新时候是用不到减的数的。

Code

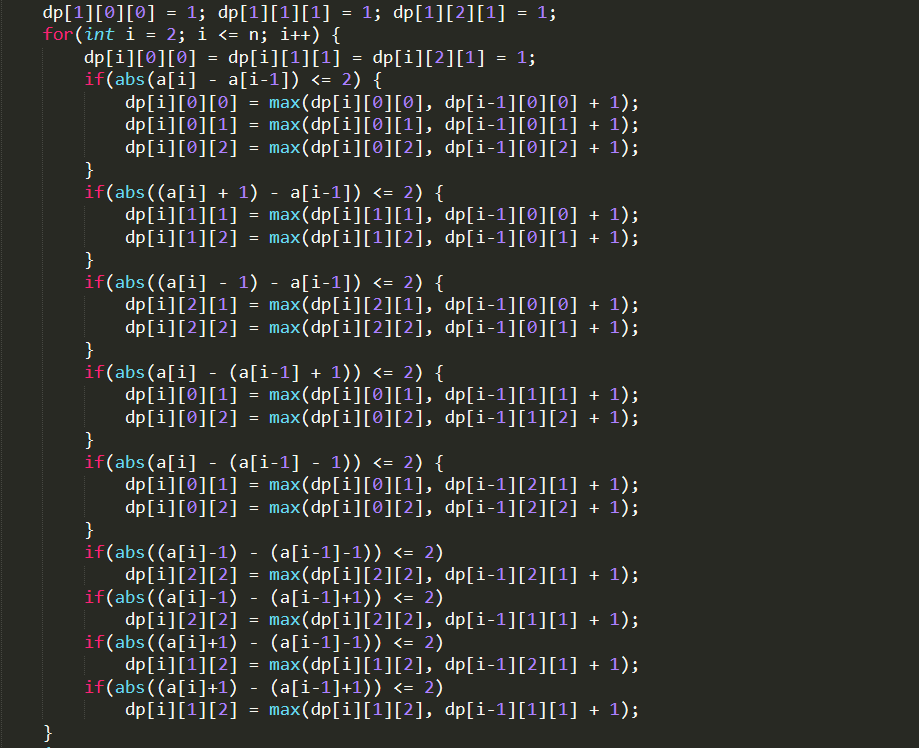
解法1代码如下：

#include <bits/stdc++.h>
using namespace std;
#define maxn 105
int n, a[maxn], dp[maxn][3][3];
int main() {
    int t;
    cin >> t;
    for (int tt = 1; tt <= t; tt++) {
        cin >> n;
        for (int i = 1; i <= n; i++) cin >> a[i];
        sort(a + 1, a + 1 + n);
        int ans = 1;
        dp[1][0][1] = dp[1][1][0] = dp[1][1][2] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j <= 2; j++) {
                if (j == 0) {  //到i一次也没有改的情况
                    if (a[i] - a[i - 1] <= 2) dp[i][0][1] = dp[i - 1][0][1] + 1;
                    else dp[i][0][1] = 1;
                    continue;
                }
                //剩下的是有改动的情况
                for (int k = 0; k <= 2; k++) {
                    dp[i][j][k] = 1;
                    for (int l = 0; l <= 2; l++) {
                        int ai = a[i] - k + 1, aj = a[i - 1] - l + 1;  //两个数改动后的值
                        //不改动a[i]的情况
                        if (k == 1) {  //这里不会出现冗余态：转移必定合法
                            if (a[i] - aj <= 2)
                                dp[i][j][1] = max(dp[i][j][1], dp[i - 1][j][l] + 1);  //注意：如果从不存在的状态推过来，就是0+1的形式
                            continue;
                        }
                        //改动a[i]的情况：这里会出现冗余态，dp[i-1][0][0|2]的状态是不存在的
                        if (ai - aj <= 2) dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - 1][l] + 1);
                    }
                }
            }
            for (int j = 0; j <= 2; j++)
                for (int k = 0; k <= 2; k++) ans = max(ans, dp[i][j][k]);
        }
        printf("Case %d: %d\n", tt, ans);
    }
}

解法2代码如下：

int a[maxn], dp[2][maxn][3];
int32_t main() {
    close;
    CASET {
        int n;
        cin >> n;
        for (int i = 1; i <= n; i++) cin >> a[i];
        sort(a + 1, a + n + 1);
        memset(dp, 0, sizeof(dp));
        int ans = 0;
        for (int i = n; i >= 1; i--) {
            int &cur = a[i];
            int now = i & 1, last = !(i & 1);
            for (int j = cur - 1; j <= cur + 1; j++){
                for (int k = 0; k <= 2; k++){
                    dp[now][j][k] = 0;
                }
            }
            for (int j = cur - 1; j <= cur + 1; j++) {
                dp[now][cur - 1][1] = max(dp[now][cur - 1][1], dp[last][j][0] + 1);
                dp[now][cur - 1][2] = max(dp[now][cur - 1][2], dp[last][j][1] + 1);
            }
            for (int j = cur; j <= cur + 2; j++) {
                dp[now][cur][0] = max(dp[now][cur][0], dp[last][j][0] + 1);
                dp[now][cur][1] = max(dp[now][cur][1], dp[last][j][1] + 1);
                dp[now][cur][2] = max(dp[now][cur][2], dp[last][j][2] + 1);
            }
            for (int j = cur + 1; j <= cur + 3; j++) {
                dp[now][cur + 1][1] = max(dp[now][cur + 1][1], dp[last][j][0] + 1);
                dp[now][cur + 1][2] = max(dp[now][cur + 1][2], dp[last][j][1] + 1);
            }
            for (int j = cur - 1; j <= cur + 1; j++)
                for (int k = 0; k <= 2; k++) ans = max(ans, dp[now][j][k]);
        }
        cout << "Case " << __CS << ": " << ans << endl;
    }
    return 0;
}

后记

暴力处理所有情况： if-else 大法好。如sol1。

zby🐂🍺